Economía y coronavirus
16 marzo, 2020 coronavirus
coronavirusHoy la urgencia sanitaria por la crisis del coronavirus y las medidas de salud pública van por delante de todo, como es natural. Este es ahora el asunto más apremiante.
De todos modos, hay que conservar la perspectiva. En cuanto al futuro, parece difícil que más adelante no haya una determinada controversia sobre los daños y los costes del Covid-19. Se producirán de todo tipo -personales, laborales, económicos, sociales y aún otros- y la discusión puede que no sea sólo sobre la magnitud y la forma de corregirlos, sino también sobre la forma en que se deberán distribuir entre el conjunto de la sociedad. Aunque son recientes, y abiertas, las asimetrías con que operó la crisis iniciada en 2008 y sus efectos sobre la desigualdad. Además, desde hace dos días la epidemia es oficialmente un asunto de interés público -esto significa el recientísimo estado de alarma en España y las peticiones de cierre de Cataluña-, con el consiguiente cambio de lógica y de criterios de valoración. Anticipo una discusión difícil y áspera de política económica y social. Ya veremos, porque estimaciones de costes que una semana atrás parecían tremendas ahora nos dan la impresión de modestas, como de mínimos.
El uso de modelos para calcular la propagación de epidemias
Mientras tanto, quisiera hacer énfasis en una circunstancia menos ruidosa. Es el hecho de que, en epidemiología, hay una determinada cantidad de modelos que describen la forma en que se propagan las enfermedades. La primera impresión es que estos modelos son de poco interés para los economistas, que pertenecen a áreas de conocimiento muy alejadas de su campo de trabajo. Parece que contagios y epidemias son asuntos propios de la medicina y de la salud pública, y que sólo se relacionan con la economía de forma indirecta, a través de los costes que generan.
Pues bien, esto no es cierto del todo. A menudo la forma como los economistas explicamos la difusión de las innovaciones tecnológicas nos viene de la biología y de la física. Más exactamente, los modelos matemáticos de propagación de epidemias, como la producida por este virus subrepticio que nos ronda. La banca digital, el comercio electrónico, el teléfono móvil y el motor Wankel han sido nuevas formas de hacer cosas que, más o menos, ya se hacían de otra forma. A veces han funcionado, otras no. ¿De qué manera describiría la difusión y la competencia entre estándares técnicos? ¿Y los procesos de adopción de nuevos productos? Como no tendríais datos sobre el pasado sólo le quedaría ir hacia el futuro. Probablemente lo primero que le vendría a la cabeza es recurrir a un modelo de competencia al modo logística, o tal vez a la Gompertz, o aprovechar el modelo depredador-presa de Alfred J. Lotka (1910) y Vito Volterra (1926), y todo ello son herramientas muy usadas en biología. Tanto se daría cambiar las especies animales para variedades de productos.


Además, en este mundo nuestro de expansión de la economía digital y de las TIC también podría pasar que te Topares con alguna externalidad de red. La rivalidad entre redes sociales ilustra la idea de que muchos productos son valiosos sobre todo por la cantidad de gente que los usa. Es lo que ocurre con WhatsApp. La idea de masa crítica, tan propia de la biología, es aquí muy importante. Cuando uno se despista se encuentra pensando en situaciones en las que el tiempo es una variable esencial -como sucede en los biólogos, o los físicos-, y en eso los economistas llevamos ventaja. Mientras que los físicos aún discuten si es posible viajar en el tiempo, nosotros trasladamos dinero del futuro hacia el presente con normalidad. Lo llamamos préstamos y los usamos desde hace milenios.
Los economistas tenemos el tiempo empotrado en la forma como vemos el mundo, pero no sé si lo aprovechamos bastante bien. Todo tiene sus servidumbres, y por remover este tipo de modelos necesitaríamos saber más de ecuaciones diferenciales y también, en cuanto las cosas se complican, de redes y de probabilidad.
El modelo SIR
Para animaros a avanzar por este camino, quisiera ilustrar aquí brevemente un modelo muy conocido de difusión de epidemias. Tiene casi cien años, se llama SIR y lo debemos a un par de escoceses, dedos William Ogilvy Kermack (1898-1970) y Anderson Gray McKendrick (1876-1943). Describe la transición de los individuos de una población de un estado denominado Susceptible (S, o Sa) a otro de Infectado (I) y de éste al de Resistente (R, o Recuperado). Es un modelo que no está exento de complicaciones pero que en la práctica, y admitiendo ciertas licencias más o menos disculpables, puede ser aproximado muy fácilmente con una hoja de cálculo. Ha sido ensayado en entornos muy diferentes, y bajo ciertos supuestos funciona bien.


Sea una determinada población total, N, que se supone constante y distribuida a cada momento del tiempo en los tres grupos citados:
N = S(t) + I(t) + R(t)
La forma cómo varía el número de miembros de cada grupo en el tiempo, esto es, la derivada en t de S (t), de I (t) y de I (t) queda descrita por las siguientes tres ecuaciones:
dS(t)/dt = – βS(t)I(t)
dI(t)/dt = βS(t)I(t) – γI(t)
dR(t)/dt = γI(t)
El parámetro beta (β) es la probabilidad de contagio en un contacto, y el parámetro gamma (γ) es el coeficiente de recuperación. Su valor es el inverso del tiempo medio que dura la enfermedad -a mayor tiempo de enfermedad, menor coeficiente de recuperación. La suma de las tres ecuaciones es nula, lo que indica que la población total se mantiene en efecto constante:
dS(t)/dt + dI(t)/dt + dR(t)/dt = d[S(t)+I(t)+R(t)]/dt = dN(t)/dt = 0
Por tanto, el modelo asume que no hay muertos, nacimientos ni movimientos migratorios (que son algo diferente de la movilidad de las personas) mientras dura la epidemia, que su magnitud es pequeña respecto al tamaño de la población, o que son de tal manera que unos compensan exactamente los otros. Este supuesto no es absurdo a corto plazo y con enfermedades de baja mortalidad sobre poblaciones grandes.
El significado de las tres ecuaciones es bastante intuitivo:
- Primera equació: el nombre de persones sanes tendeix a disminuir amb el temps (signe negatiu) de forma proporcional al nombre de contactes entre les persones sanes i les infectades.
- Segona equació: el nombre de persones infectades augmenta a causa dels sans que emmalalteixen, i disminueix pels malalts que es curen.
- Tercera equació: el nombre de persones resistents tendeix a créixer de forma sistemàtica (signe positiu), proporcional al nombre de persones infectades. Els recuperats es converteixen en resistents al virus i no tornen a emmalaltir.
- Primera ecuación: el número de personas sanas tiende a disminuir con el tiempo (signo negativo) de forma proporcional al número de contactos entre las personas sanas y las infectadas.
- Segunda ecuación: el número de personas infectadas aumenta debido a los sanos que enferman, y disminuye los enfermos que se curan.
- Tercera ecuación: el número de personas resistentes tiende a crecer de forma sistemática (signo positivo), proporcional al número de personas infectadas. Los recuperados se convierten en resistentes al virus y no vuelven a enfermar.
Hasta aquí el modelo SIR. Es sencillo ilustrarlo en una hoja de cálculo. Basta fijar unos valores para los parámetros beta (β) y gamma (γ), un número inicial de personas sanas y otro de personas infectadas.
¿Podemos aplicar el modelo SIR con los datos actuales del COVID19?
En nuestro caso tomaremos como datos unas cifras inventadas. Sean los valores:
| beta | 0,0001 | |||
| gamma | 0,2500 | |||
| N | 5.000,00 | |||
| t | Sanos | Infectados | Resistentes | N |
| 0 | 4.900 | 100 | 0 | 5.000 |
Escriba a continuación las fórmulas del modelo para el período t = 1 (podemos tomar los períodos t como días). Son las siguientes:
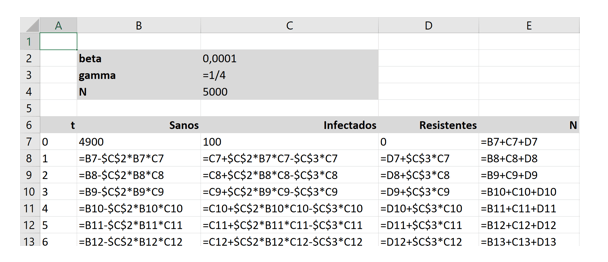
Las fórmulas reproducen directamente las tres ecuaciones de flujo vistas, aunque en términos discretos en vez de continuos. La población total (N) se obtiene por suma.
Copie en su hoja de cálculo sólo las fórmulas correspondientes a la fila del momento t = 1. Las otras no será necesario, se muestran aquí sólo por claridad. Escrita la primera fila, la correspondiente a t = 1, bastará arrastrar las celdas hacia abajo. Esto replicará de forma automática las fórmulas, sin necesidad de escribirlas. En dos minutos estará todo hecho, y tendremos sin esfuerzo el resultado siguiente:
| beta | 0,0001 | |||
| gamma | 0,2500 | |||
| N | 5000,00 | |||
| t | Sanos | Infectados | Resistentes | N |
| 0 | 4.900 | 100 | 0 | 5.000 |
| 1 | 4.851 | 124 | 25 | 5.000 |
| 2 | 4.791 | 153 | 56 | 5.000 |
| 3 | 4.717 | 188 | 94 | 5.000 |
| 4 | 4.629 | 230 | 141 | 5.000 |
| 5 | 4.522 | 279 | 199 | 5.000 |
| 6 | 4.396 | 335 | 269 | 5.000 |
| 7 | 4.249 | 399 | 352 | 5.000 |
| 8 | 4.079 | 469 | 452 | 5.000 |
| 9 | 3.888 | 543 | 569 | 5.000 |
No se detenga al día 9, siga arrastrando celdas hasta más abajo, ya que con nuestros datos son necesarios un poco más de dos meses (de hecho, 65 días) para que la epidemia desaparezca.
Si a continuación hacemos un gráfico con las series de Sanos, de Infectados y de Resistentes tendrá el siguiente:
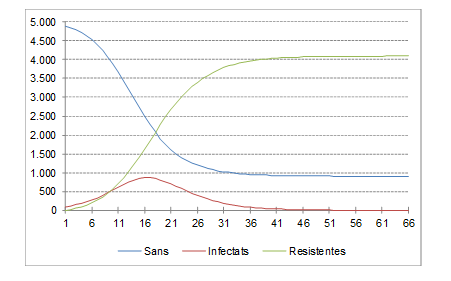
Ya veis … el número de infectados crece al principio muy deprisa, alcanza el número máximo al cabo de 15 o 16 días (con 867 infectados, en rojo) y después tiende a remitir. El número de personas inicialmente sanas (en azul) tiende a disminuir, porque conforme se infectan y se recuperan de la enfermedad se inmuniza frente al virus. Son las personas resistentes, en verde, que siguen una línea creciente. En todos los períodos la población total se mantiene constante (5.000 persona)
Construido el modelo, es sencillísimo sustituir los valores iniciales de beta y gamma por otros valores diferentes para ver qué efectos tiene esto sobre el número de personas que hay en cada estado, y el calendario de propagación de la enfermedad. Por ejemplo, aumente el valor de beta hasta 0,00015 (mayor probabilidad de contagio) al tiempo que reduzca el valor de gama hasta 0,2 (alargamiento medio de la enfermedad de 4 días a 5). De forma automática la hoja de cálculo revisará todos los resultados y verá que con estos pequeños cambios el número máximo de infectados crece y se produce con mayor rapidez, al tiempo que la epidemia termina antes. En otras palabras, los resultados del modelo son muy sensibles a los valores de los parámetros beta y de gama.
Un escenario real aún no definido
En la práctica, el valor de gamma probablemente se puede estimar bastante bien. En todo caso, con más facilidad que el de beta. Este último parámetro, si se piensa un poco, será difícil de obtener a la realidad. Ni siquiera es seguro que sea constante en el tiempo. Las medidas de salud pública tienden a reducir la tasa de contagio, a reducir beta de forma artificial a través de medidas de higiene, del cierre de fronteras, de cines y teatros, de escuelas, de centros de trabajo, de la obligatoriedad respetar medidas de cuarentena y aislamiento, de la suspensión de ferias como el Mobile World Congress, de actos deportivos de masas, de fiestas populares y otras actividades que aglomeran personas. También reducen beta las restricciones sobre viajes a determinados destinos y otras limitaciones de la movilidad de la población, ya sean dentro del mismo país (pongamos, por movilidad obligada por trabajo o estudios) o entre países (pongamos, por turismo).
Una posibilidad es definir varios escenarios a partir de hipótesis sobre el comportamiento de los parámetros. Como escenario base podemos tomar el de nuestro primer ejemplo (beta = 0,0001, gamma = 0,025), como escenario optimista una reducción de beta hasta 0,00007 e igual gama, y como escenario pesimista un aumento de beta hasta 0,00015 y un aumento de la duración de la enfermedad de 4 a 5 días (gama = 0,2). Los cambios parecen pequeños, pero el número de personas infectadas en cada caso y el calendario de infecciones son bastante diferentes:
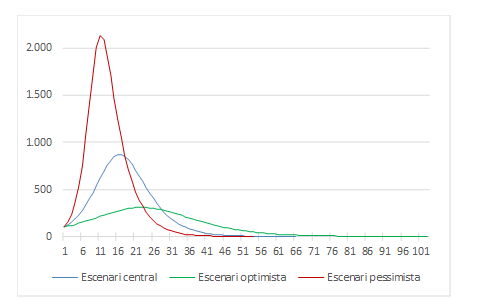
Para terminar, una observación importante: tened en cuenta que la primera ecuación del modelo contiene un supuesto crítico: las personas sanas y las infectadas se comportan como bolas dentro de un bombo, todo el mundo puede tener contacto con todo el mundo y propagar la epidemia. Este supuesto es realista en entornos relativamente pequeños y cerrados (un barco, un internado, una comunidad, etc.)..
Pero en un colectivo realmente grande (un país) habría que introducir dentro del modelo alguna medida de las pautas de movilidad de la población por ocio, por trabajo, por estudio … Si no tenemos esto presente, aceptaremos que personas de dos territorios distantes se pueden contagiar entre sí como si fueran vecinas, y el modelo tenderá a exagerar el número de contagios. En realidad, la probabilidad de contacto entre personas no es igual en todos los casos. Además, ya se ha dicho que estas pautas de movilidad pueden no ser constantes mientras dura la epidemia, ya sea por la prudencia de los individuos o por las restricciones a su movilidad ya citadas.
En fin, si os apetece, ya veis que se os gira trabajo. En particular, y una vez ensayadas varias combinaciones de beta y gamma, decid: cómo debe ser γ / β para que la epidemia se extinga sola?






Excelenet nota
Consulta, ¿como se puede estimar el beta del modelo dado los datos disponibles de la propagacion del covid para cada region?
¿Se realiza a traves de regresiones como hacemos los economistas en econometria?
Desde ya mucahs graicas, saludos