Economia i coronavirus
16 març, 2020 coronavirus
coronavirusAvui la urgència sanitària per la crisi del coronavirus i les mesures de salut pública van per davant de tot, com és natural. Aquest és ara l’assumpte més peremptori.
De tota manera, cal conservar la perspectiva. Quant al futur, sembla difícil que més endavant no hi hagi una determinada controvèrsia sobre els danys i els costos del Covid-19. Se’n produiran de tota mena —personals, laborals, econòmics, socials i encara d’altres— i la discussió potser no serà només sobre la magnitud i la forma de corregir-los, sinó també sobre la forma com s’hauran de distribuir entre el conjunt de la societat. Encara són recents, i obertes, les asimetries amb què va operar la crisi engegada el 2008 i els seus efectes sobre la desigualtat. A més, des de fa dos dies l’epidèmia és oficialment un afer d’interès públic —això vol dir el recentíssim estat d’alarma a Espanya i les peticions de tancament de Catalunya—, amb el consegüent canvi de lògica i de criteris de valoració. Anticipo una discussió difícil i aspra de política econòmica i social. Ja veurem, perquè estimacions de costos que una setmana enrere semblaven tremendes ara ens fan l’efecte de modestes, com de mínims.
L’ús de models per calcular la propagació d’epidèmies
Mentrestant, voldria fer èmfasi en una circumstància menys sorollosa. És el fet que, en epidemiologia, hi ha una determinada quantitat de models que descriuen la forma com es propaguen les malalties. La primera impressió és que aquests models són de poc interès per als economistes, que pertanyen a àrees de coneixement molt allunyades del seu camp de treball. Sembla que contagis i epidèmies són assumptes propis de la medicina i de la salut pública, i que només es relacionen amb l’economia de forma indirecta, a través dels costos que generen.
Doncs bé, això no és cert del tot. Sovint la forma com els economistes expliquem la difusió de les innovacions tecnològiques ens ve de la biologia i de la física. Més exactament, dels models matemàtics de propagació d’epidèmies, com ara la produïda per aquest virus subreptici que ens ronda. La banca digital, el comerç electrònic, el telèfon mòbil i el motor Wankel han estat noves formes de fer coses que, si fa o no fa, ja es feien d’altra forma. A vegades han funcionat, d’altres no. De quina manera descriuríeu la difusió i la competència entre estàndards tècnics? I els processos d’adopció de nous productes? Com que no tindríeu dades sobre el passat només us quedaria anar cap al futur. Probablement el primer que us vindria al cap és recórrer a un model de competència a la manera logística, o potser a la Gompertz, o aprofitar el model depredador-presa d’Alfred J. Lotka (1910) i Vito Volterra (1926), i tot això són eines molt usades a biologia. Tant se’n donaria canviar les espècies animals per varietats de productes.


A més, en aquest món nostre d’expansió de l’economia digital i de les TIC també podria passar que us topéssiu amb alguna externalitat de xarxa. La rivalitat entre xarxes socials il·lustra la idea que molts productes són valuosos sobretot per la quantitat de gent que els usa. És el que passa amb WhatsApp. La idea de massa crítica, tan pròpia de la biologia, és aquí molt important. Quan un es despista es troba pensant en situacions en les quals el temps és una variable essencial —com passa als biòlegs, o als físics—, i en això els economistes portem avantatge. Mentre que els físics encara discuteixen si és possible viatjar en el temps, nosaltres traslladem diners del futur cap al present amb normalitat completa. En diem préstecs i els usem des de fa mil·lennis.
Els economistes tenim el temps encastat en la forma com veiem el món, però no sé si ho aprofitem prou bé. Tot té les seves servituds, i per remenar aquesta mena de models ens caldria saber més d’equacions diferencials i també, de seguida que les coses es compliquen, de xarxes i de probabilitat.
El model SIR
Per tal d’animar-vos a avançar per aquest camí, voldria il·lustrar aquí breument un model molt conegut de difusió d’epidèmies. Té gairebé cent anys, s’anomena SIR i el devem a un parell d’escocesos, dits William Ogilvy Kermack (1898-1970) i Anderson Gray McKendrick (1876-1943). Descriu la transició dels individus d’una població d’un estat denominat Susceptible (S, o Sa) a un altre d’Infectat (I) i d’aquest al de Resistent (R, o Recuperat). És un model que no està exempt de complicacions però que en la pràctica, i admetent certes llicències més o menys disculpables, pot ser aproximat molt fàcilment amb un full de càlcul. Ha estat assajat en entorns molt diferents, i sota certs supòsits funciona bé.


Sigui una determinada població total, N, que se suposa constant i distribuïda a cada moment del temps en els tres grups citats:
N = S(t) + I(t) + R(t)
La forma com varia el nombre de membres de cada grup en el temps, això és, la derivada en t de S(t), de I(t) i de R(t) queda descrita per les següents tres equacions:
dS(t)/dt = – βS(t)I(t)
dI(t)/dt = βS(t)I(t) – γI(t)
dR(t)/dt = γI(t)
El paràmetre beta (β) és la probabilitat de contagi en un contacte, i el paràmetre gamma (γ) és el coeficient de recuperació. El seu valor és l’invers del temps mitjà que dura la malaltia —a major temps de malaltia, menor coeficient de recuperació. La suma de les tres equacions és nul·la, cosa que indica que la població total es manté en efecte constant:
dS(t)/dt + dI(t)/dt + dR(t)/dt = d[S(t)+I(t)+R(t)]/dt = dN(t)/dt = 0
Per tant, el model assumeix que no hi ha morts, naixements ni moviments migratoris (que són una cosa diferent de la mobilitat de les persones) mentre dura l’epidèmia, que la seva magnitud és petita respecte a la grandària de la població, o que són de tal mena que uns compensen exactament els altres. Aquest supòsit no és absurd a curt termini i amb malalties de baixa mortalitat sobre poblacions grans.
El significat de les tres equacions és bastant intuïtiu:
- Primera equació: el nombre de persones sanes tendeix a disminuir amb el temps (signe negatiu) de forma proporcional al nombre de contactes entre les persones sanes i les infectades.
- Segona equació: el nombre de persones infectades augmenta a causa dels sans que emmalalteixen, i disminueix pels malalts que es curen.
- Tercera equació: el nombre de persones resistents tendeix a créixer de forma sistemàtica (signe positiu), proporcional al nombre de persones infectades. Els recuperats es converteixen en resistents al virus i no tornen a emmalaltir.
Fins aquí el model SIR. És senzill il·lustrar-lo en un full de càlcul. Basta fixar uns valors per als paràmetres beta (β) i gamma (γ), un nombre inicial de persones sanes i un altre de persones infectades.
Podem aplicar el model SIR amb les dades actuals del COVID19?
En el nostre cas prendrem com a dades unes xifres inventades. Siguin els valors:
| beta | 0,0001 | |||
| gamma | 0,2500 | |||
| N | 5.000,00 | |||
| t | Sans | Infectats | Resistents | N |
| 0 | 4.900 | 100 | 0 | 5.000 |
Escriviu a continuació las fórmules del model per al període t=1 (podem prendre els períodes t com a dies). Són les següents:
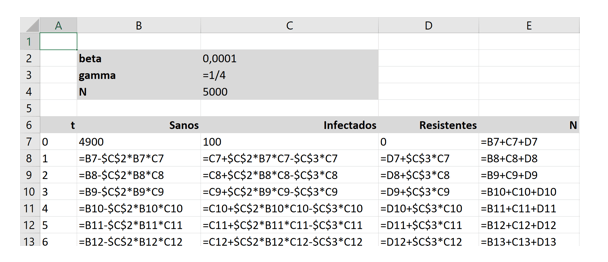
Les fórmules reprodueixen directament les tres equacions de flux vistes, encara que en termes discrets en comptes de continus. La població total (N) s’obté per suma.
Copieu en el vostre full de càlcul només les fórmules corresponents a la fila del moment t=1. Les altres no serà necessari, es mostren aquí només per claredat. Escrita la primera fila, la corresponent a t=1, bastarà arrossegar les cel·les cap avall. Això replicarà de forma automàtica les fórmules, sense necessitat d’escriure-les. En dos minuts estarà tot fet, i tindrem sense esforç el resultat següent:
| beta | 0,0001 | |||
| gamma | 0,2500 | |||
| N | 5000,00 | |||
| t | Sans | Infectats | Resistents | N |
| 0 | 4.900 | 100 | 0 | 5.000 |
| 1 | 4.851 | 124 | 25 | 5.000 |
| 2 | 4.791 | 153 | 56 | 5.000 |
| 3 | 4.717 | 188 | 94 | 5.000 |
| 4 | 4.629 | 230 | 141 | 5.000 |
| 5 | 4.522 | 279 | 199 | 5.000 |
| 6 | 4.396 | 335 | 269 | 5.000 |
| 7 | 4.249 | 399 | 352 | 5.000 |
| 8 | 4.079 | 469 | 452 | 5.000 |
| 9 | 3.888 | 543 | 569 | 5.000 |
No us atureu al dia 9, seguiu arrossegant cel·les fins a més a baix, ja que amb les nostres dades són necessaris una mica més de dos mesos (de fet, 65 dies) perquè l’epidèmia desaparegui.
Si a continuació feu un gràfic amb les sèries de Sans, d’Infectats i de Resistents tindreu el següent:
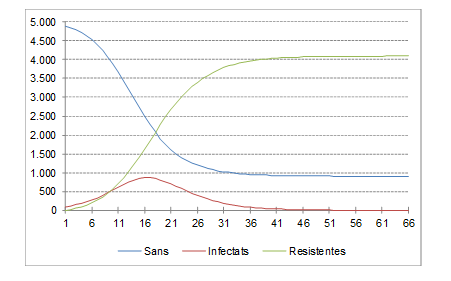
Ja veieu… el nombre d’infectats creix al principi molt de pressa, arriba al nombre màxim al cap de 15 o 16 dies (amb 867 infectats, en vermell) i després tendeix a remetre. El nombre de persones inicialment sanes (en blau) tendeix a disminuir, perquè conforme s’infecten i es recuperen de la malaltia s’immunitzen davant al virus. Son les persones resistents, en verd, que segueixen una línia creixent. En tots els períodes la població total es manté constant (5.000 persones).
Construït el model, és senzillíssim substituir els valors inicials de beta i gamma per altres valors diferents per veure quins efectes té això sobre el nombre de persones que hi ha en cada estat, i el calendari de propagació de la malaltia. Per exemple, augmenteu el valor de beta fins a 0,00015 (major probabilitat de contagi) alhora que reduïu el valor de gamma fins a 0,2 (allargament mitjà de la malaltia de 4 dies a 5). De forma automàtica el full de càlcul revisarà tots els resultats i veureu que amb aquests petits canvis el nombre màxim d’infectats creix i es produeix amb major rapidesa, alhora que l’epidèmia acaba abans. En altres paraules, els resultats del model són molt sensibles als valors dels paràmetres beta i de gamma.
Un escenari real encara no definit
En la pràctica, el valor de gamma probablement es pot estimar bastant bé. En tot cas, amb més facilitat que el de beta. Aquest últim paràmetre, si es pensa una mica, serà difícil d’obtenir a la realitat. Ni tan sols és segur que sigui constant en el temps. Les mesures de salut pública tendeixen a reduir la taxa de contagi, a reduir beta de forma artificial a través de mesures d’higiene, del tancament de fronteres, de cinemes i teatres, d’escoles, de centres de treball, de l’obligatorietat de respectar mesures de quarantena i aïllament, de la suspensió de fires com el Mobile World Congress, d’actes esportius de masses, de festes populars i d’altres activitats que aglomeren persones. També redueixen beta les restriccions sobre viatges a determinades destinacions i altres limitacions de la mobilitat de la població, ja siguin dins del mateix país (posem, per mobilitat obligada per treball o estudis) o entre països (posem, per turisme).
Una possibilitat és definir diversos escenaris a partir d’hipòtesis sobre el comportament dels paràmetres. Como escenari base podem prendre el del nostre primer exemple (beta=0,0001, gamma=0,025), com a escenari optimista una reducció de beta fins a 0,00007 i igual gamma, i com a escenari pessimista un augment de beta fins a 0,00015 i un augment de la durada de la malaltia de 4 a 5 dies (gamma=0,2). Els canvis semblen petits, però el nombre de persones infectades en cada cas i el calendari d’infeccions són prou diferents:
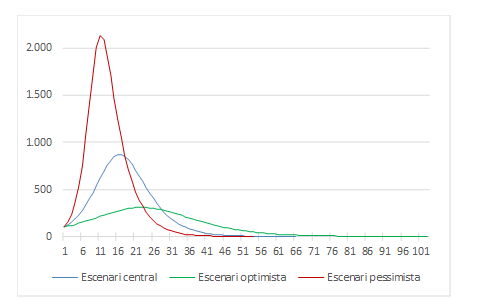
Per acabar, una observació important: fixeu-vos que la primera equació del model conté un supòsit crític: les persones sanes i les infectades es comporten com boles dins d’un bombo, tothom pot tenir contacte amb tothom i propagar l’epidèmia. Aquest supòsit és realista en entorns relativament petits i tancats (un vaixell, un internat, una comunitat, etc.).
Però en un col·lectiu realment gran (un país) caldria introduir dins el model alguna mesura de les pautes de mobilitat de la població per oci, per treball, per estudi… Si no tenim això present, acceptarem que persones de dos territoris distants es poden contagiar entre si com si fossin veïnes, i el model tendirà a exagerar el nombre de contagis. En realitat, la probabilitat de contacte entre persones no és igual en tots els casos. A més, ja s’ha dit que aquestes pautes de mobilitat poden no ser constants mentre dura l’epidèmia, ja sigui per la prudència dels individus o per les restriccions a la seva mobilitat ja citades.
En fi, si us ve de gust, ja veieu que se us gira feina. En particular, i un cop assajades diverses combinacions de beta i gamma, digueu: com ha de ser γ/β per tal que l’epidèmia s’extingeixi sola?





